O triângulo milagroso

Afinal a matemática é mesmo uma batata?!
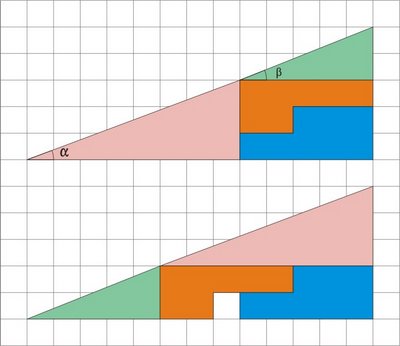
Recebi há dias um desafio interessante: "como se pode ver nesta imagem, o triângulo de cima é decomposto em quatro figuras. Rearranjando-as (no triângulo de baixo), elas ocupam a mesma área mas... sobra um quadradinho vazio".
Milagre?!
A matemática é uma batata?!
Claro que não. Temos aqui uma bela falácia. É que o que nos dizem que é um triângulo... não é! Se fosse, a hipotenusa seria um segmento de recta. E, nesse caso, os ângulos Alfa e Beta (que assinalei na figura de cima) teriam a mesma inclinação. Mas façam as contas:

• tg Alfa = 3/8 = 0,375. Ou seja, o ângulo Alfa mede 21º.


• tg Beta = 2/5 = 0,4. Ou seja, o ângulo Beta mede 22º.

Se ligarem os extremos do triângulo, o que parece a hipotenusa reparte-se afinal em dois segmentos de recta de inclinações diferentes. Quase não se nota... pelo que é muito fácil cair-se na esparrela.
Assim, a área do quadradinho vazio no «triângulo» de baixo corresponde à área que falta ao que seria um verdadeiro triângulo de cima mais a área que o «triângulo» de baixo tem a mais em relação à hipotenusa de um verdadeiro triângulo.
É bom continuar a saber que a matemática não é uma batata!

Entretanto, agradeço ao meu primo Nuno, que me mandou este link para uma página de matemática onde se apresenta um exemplo idêntico do que chamam «falácia da dissecção»:

"Uma falácia de dissecção é um paradoxo aparente que surge quando duas figuras planas com diferentes áreas parecem ser compstas pelo mesmo conjunto finito de partes. Para produzir esta ilusão, as peças devem ser cortadas e reagrupadas de forma a que a parte em falta ou excedente fique escondida por imperfeições de forma minúsculas e negligenciáveis. Um exemplo claro e revelador pode ser construido cortando um quadrado de 8 x 8 da forma apresentada na figura da esquerda:
As figuras do meio e do centro parecem demonstrar que as mesmas peças podem dar origem a dois diferentes polígonos, com áreas de 5 x 13 = 65 e 2 (5 x 6) + 3 = 63, respectivamente. Isto implicaria que 63 = 64 = 65!
No entanto, uma observação mais atenta aos lados inclinados das peças trapezoidais e triangular mostram que elas não podem ser alinhadas como se fez nas ilustrações de cima. De facto, são diagonais de dois rectângulos não idênticos, de dimensões 2 x 5 e 3 x 8, respectivamente, pelo que têm diferentes inclinações. Mas as diferenças entre os rácios ( 2/5=0,4 e 3/8=0,375) é tão pequena que nem se consegue aperceber visualmente.
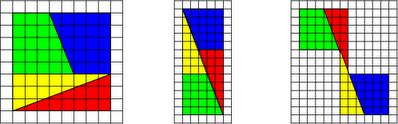
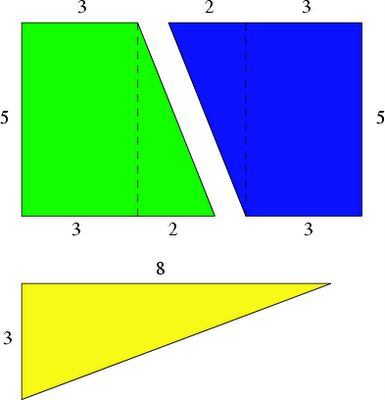
Note-se que a dissecção neste exemplo cortou o quadrado 8 x 8 na proporção 5:3. A ilusão ainda se torna mais eficaz se os números 3, 5 e 8 forem substituídos por um trio de números de Fibonacci maiores e consecutivos."